Wollermann, Tobias: Musik und Medium

beschrieben. An der Stelle, wo sich zwei Tangenten schneiden, erhält man einen Kontrollpunkt. Dieser hat einen entsprechenden Punkt auf der Kurve, an dem nun wiederum eine Tangente angelegt werden kann, die sich wieder mit den beiden bereits existierenden Tangenten schneidet, zwei neue Kontrollpunkte bildet etc.

Generell kann ein Bézier-Kurvenausschnitt an eine beliebige Anzahl von Kontrollpunkten angepasst werden. Dabei bestimmen die Anzahl der Kontrollpunkte sowie die relative Lage der Punkte zueinander den Grad des Bézier-Polynoms.

Existieren n + 1 Kontrollpunkte p_k = (x_k,y_k,z_k) und k variiert von 0 bis n, dann können diese Kontrollpunkte vermischt (blended) werden. Dadurch erhält man den Positionsvektor P(u), der den Weg einer angenäherten Bézier-Funktion zwischen p₀ und p_n beschreibt:

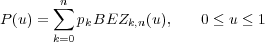∑n P (u) = pkBEZk,n (u), 0 ≤ u ≤ 1 k=0

(10.13)

Dabei wird p_k mit Hilfe eines Bernstein-Polynoms BEZ_k,n(u) gewichtet:

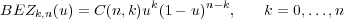BEZk,n (u) = C (n,k)uk(1- u)n-k, k = 0,...,n

(10.14)

wobei C(n,k) die Binomialkoeffizienten darstellen:

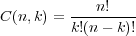n! C (n,k) =--------- k!(n - k)!

(10.15)

Die Auswertung der Bernstein-Polynome erweist sich als äußerst komplex. Der Franzose de Casteljau schlug deshalb ein Iterationsverfahren vor, welches durch fortgesetztes Zerteilen von Linien den gewünschten Kurvenpunkt approximieren kann:

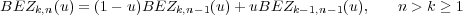BEZk,n (u) = (1 - u)BEZk,n-1(u)+ uBEZk - 1,n-1(u), n > k ≥ 1

(10.16)

Dabei ist BEZ_k,k = u^k, und BEZ_0,k = (1 - u)^k.

Die Vektordarstellung 10.13 liefert drei parametrische Ausdrücke für die individuellen Kurvenkoordinaten:

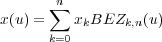∑n x(u ) = xkBEZk,n (u) k=0

(10.17)

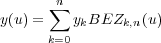∑n y(u ) = ykBEZk,n (u) k=0

(10.18)

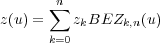∑n z(u) = zkBEZk,n(u) k=0

(10.19)

In der Regel ist der Grad des Polynoms immer eine Einheit niedriger als die Anzahl der benutzen Kontrollpunkte: drei Punkte generieren eine Parabel, vier Punkte eine kubische Kurve, etc. Eine effektive Methode, um die Koordinaten entlang einer Bézier-Kurve zu bestimmen, ist die rekursive Kalkulation. Z. B. können sukzessive Binomialkoeffizienten mit