Weyde, Tillman: Lern- und wissensbasierte Analyse von Rhythmen

Abbildung 5.5:

Dreiecks-Funktion, Trapez-Funktion und Gaußfunktion

5.2.2. Fuzzy-Operatoren

Der Übergang von Mengen zur Prädikatenlogik ergibt sich aus der Äquivalenz eines Prädikats P(x) zu der Zugehörigkeit von x zur Menge aller Objekte, für die P gilt. Man kann für eine Menge A die Zugehörigkeit _A(x) als Wahrheitswert der Aussage P(x) mit P(x) <==> x A auffassen, und man kann statt von Zugehörigkeitswerten auch von Wahrheitswerten sprechen. Sei A eine Fuzzy-Menge über der Grundmenge X mit der ZGF _A. Dann wird mit [[]] der Wahrheitswert der atomaren Aussage X bezeichnet, der durch

[[f]] = mA(f)

definiert wird.

Entsprechend der herkömmlichen Mengenlehre kann man auf Fuzzy-Mengen die Operatoren Durchschnitt ( $/~\$ ), Vereinigung () und Komplement (^c) definieren, deren Beziehung zu logischen Operatoren sich analog zur klassischen Logik definieren läßt:

m (x) \/ m (x) = m (x) A x (- X A B A U B mA(x) /\ mB(x) = mA /~\ B(x) A x (- X (5.25) ¬ mA(x) = mAc(x).

Die Werte dieser Operatoren werden durch Auswertungsfunktionen bestimmt, die zu einem Operator

und Mengen A und B mit den ZGF

_A und

_B eine Funktion

2 mAo x B : [0,1] ---> [0,1]

darstellen, bzw. für unäre Operatoren eine Funktion

mA ox : [0,1]---> [0,1].

Für Komplement bzw. Negation sollte wie auch in der klassischen Logik ¬1 = 0 und ¬0 = 1 gelten. Zusätzlich sollten Monotonie
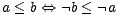$a < b <==> ¬b < ¬a$ (5.26)

und Involution
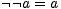$¬ ¬a = a$ (5.27)