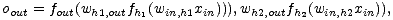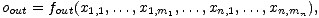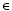Weyde, Tillman: Lern- und wissensbasierte Analyse von Rhythmen

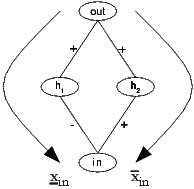
die Wirkung eines Eingabeneurons auf die Ausgabe umkehren, daher wird ggf. eine untere Grenze x_i benötigt. Im Beispiel in Abbildung 10.3 berechnet sich die Aktivierung o_out des Ausgabeneurons out als

oout = fout(wh1,outfh1(win,h1xin))),wh2,outfh2(win,h2xin)),

(10.2)

wobei f_x die durch das Neuron x berechnete mehrstellige Funktion der gewichteten Eingaben bezeichnet. Der Wert x_in taucht hier zweimal als Argument auf, da es zwei Wege durch das Netz von in nach out gibt. Allgemein kann man die Aktivierung eines Ausgabeneurons als eine mehrstellige Funktion f_out darstellen, in der jeder Weg von einem Eingabeneuron zum Ausgabeneuron einem Argument entspricht:
$oout = fout(x1,1,...,x1,m1,...,xn,1,...,xn,mn),$ (10.3)

wobei x_i,j die j-te Auswertung des Merkmals x_i bezeichnet.

Abbildung 10.3:

Abschätzung der größten möglichen Aktivierung des Ausgabeneurons.

Für jedes Argument x_i,j gibt es eine Folge W_i,j von Gewichten, die auf dem zugehörigen Weg vom Eingabe- zum Ausgabeneuron wirksam werden. Unter der Voraussetzung, daß die f_x monoton steigend in allen Argumenten sind, ist auch f_out in jedem Argument wieder monoton. Für ein Argument x_i,j ist f_out monoton steigend, wenn das Produkt prod _xW₍i,j)w_x der Gewichte, die zur Auswertung von x beitragen, positiv ist; f_out ist monoton fallend, wenn das Produkt negativ ist. Ist prod w_x⁽ⁱ⁾ = 0, dann ist f_out in der Komponente x konstant. Man erhält daher eine obere Grenze für o_out, wenn man die obere Grenze für jedes Argument getrennt bestimmt:

oout = fout(x1,1,...,x1,m1,...,xn,1,...,xn,mn), mit { xi falls alle Informationen verfü gbar xij = xi falls prod wn,mn > 0 (10.4) x- falls prod wn,m < 0. i n

Damit wird bei mehreren Wegen vom Ausgabe- zum Eingabeneuron abhängig