entlang der E-Achse dar. Eine Veränderung des Tempos entspricht einer Dilatation, wobei auch der Beginn der ersten Note verschoben wird, wenn n_E⁽¹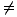⁾0 gilt. Daher wird man meist Translationen und Dilatationen zulassen. Die üblichen Gestaltabbildungen dienen dazu, die Invarianten zu einer bestimmten Abbildung zu betrachten. Für Translationen ist dies die Abbildung auf die Einsatzabstände zwischen den Noten eines Motivs, für Dilatation und Translation ist es die Abbildung auf die Relationen der Einsatzabstände.

Betrachtet man diese Abbildungen nicht in MOT, sondern in t(MOT), so ergibt sich eine weitere Abstraktionsmöglichkeit in der Anwendung eines paradigmatischen Themas P_n, d.h. einer Gruppe von Abbildungen auf G_n,t, die bezüglich eines Maßes d Isometrien sind. Ein solches paradigmatisches Thema ist die Kontrapunktgruppe die von Umkehrung und Krebsgang erzeugt wird. In der Mathematischen Musiktheorie wird die Gesamtheit aller Motive, die sich durch Anwendung von Elementen aus P ineinander überführen lassen, als Gestalt bezeichnet.²⁵

Mathematisch gesehen ist die so definierte Gestalt eines Motivs M die Bahn P_nt(M) von M:

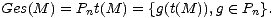(6.3)

Der Gestaltabstand zweier Gestalten G₁,G₂ wird dann definiert als das Minimum der Abstände zwischen den Elementen der Gestalten (d.h. Elementen aus Bildern von Motiven):

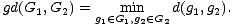(6.4)

Der Gestaltabstand beschreibt also den minimalen Abstand zweier Motive unter Anwendung bestimmter Veränderungen. Die paradigmatische Gruppe der Translationen und Dilatationen mit d als dem euklidischen Abstand der Einsatzzeiten liefert z.B. für gd den kleinsten Abstand bei optimaler zeitlicher Verschiebung. Anders ausgedrückt reduziert die Gestaltabbildung die Motive auf einen bestimmten Aspekt A, die paradigmatische Gruppe dividiert einen Teilaspekt B, z.B. die zeitliche Position, heraus. Der Gestaltabstand stellt sich dann als der geringstmögliche Abstand in einem Maß d bezüglich eines Aspekts A dar wenn man einen Aspekt B unberücksichtigt läßt, , z.B. Übereinstimmung der Einsatzzeiten wenn die zeitliche Position und die Transposition eines Motivs nicht berücksichtigt werden.

Dieser mathematische Rahmen ist sehr flexibel und gut geeignet, Ähnlichkeit unter verschiedenen Aspekten zu modellieren. Die Möglichkeit, Ähnlichkeit unabhängig von Position und Tempo zu definieren, entspricht der Fähigkeit musikalischer Hörer, die gut von diesen Größen abstrahieren können. Damit werden z.B. auch Augmentationen und Diminuitionen erfaßt oder Beziehungen zwischen Teilen in verschiedenen Tempi. Dies eröffnet die Möglichkeit, Ausführungsdaten zu verwenden und die zeitliche Gestaltung einer Interpretation zu untersuchen.

Die Information über die abweichenden Aspekte, etwa um wieviel das Tempo abweicht, wird in der Mathematischen Musiktheorie allerdings nicht berücksichtigt. Dies wäre jedoch wichtig, um z.B. das Tempo zu bewerten oder die Position, an der